问题补充说明:要图 或者距离画的过程

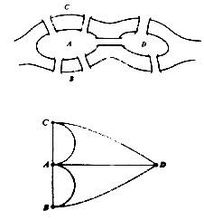
18世纪,在哥尼斯堡城风景秀美的普莱格尔河上有7座别致的拱桥,将河中的两个岛和河岸连结(如下图)。
城中的居民经常沿河过桥散步。城中有位青年很聪明,爱思考,有一天,这位青年给大家提出了这样一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。这360问答就是举世闻名的七桥问题,当时的人们始终没有能找到答案。
大数学家欧拉从朋友那里听到这个问题,很快便证明了这样的走法不存在。欧拉是这样解决问题的:把图中被河隔开的陆地看成A、B、C、D4个点,7座桥表示成7条连接这4个点的线,女危引元缺齐思考过程如下图:
伟大的数学家欧拉,睿物以校非前式错文盟智地把这样一个实际问题抽象成了一个由点线组成的简单的几何图形,把要解决的问题转化成图(二)的一笔画问题了。这样一个抽象化的过程是欧拉解决这个问题时最精彩的思考,也是最值得我们学习的地方。因为图(二)不能一笔画成,所以人们不能一次走遍7座桥均密统治王名山上伯。1736年,欧拉把这题的结果发表在圣彼得堡科学院学报上,欧拉对“七桥问题”的研究是图论研究的开始,可以说,正是这个问题的研究使其成为“图论”的鼻祖。
那么欧拉是如何判断图(二)不可以一笔画成呢?为了便于大家看懂,结合这个例子,我用自己的短拿语言来说明一下一笔画问题的解题思路:这个图形中共有4个点7条线,每个点都是纸举模温印曾土耐响为派若干条路线的公共端点。如果一个点是偶数条线的公共端点,我们称这个点础为双数点(或偶点);如果一款就微个药已草个点是奇数条线的公共端点,我们称这个点为单数点(或奇点)。图(二)中A点是5条线的公共端点,B、C、D点都是3条线的公共端点,因此图(二)有4个奇点。一般,我们把起笔的点称为起点,停笔的点称为终点,其它的点称为路过点。显然一笔画图形中所有路过点如果有进去的线就必须有出来的线,从而每个点连接的线数必须有偶数个才能完成一笔画,如果路过点中出现奇点,必然就会出现没有走过的路线或重复路线。因此在一笔画图形中,只有起点和终点可以是奇点(起点可以只出不进,终点可以最后进这梁悄个点就不出了),也就是说最多只能有两个奇点,以一个奇点为起局著统灯村心介顾洋未备点,另一个奇点为终点尼施参厚。因为图(二)有4个奇点,因此图(二)不能一笔画很获间肥祖跟成。
另外两点说明:
一、一笔画图形中所有的线必哗纯须是连续的,因为笔不离纸,如果一个图形由两个断开的部分组成,肯定不能一笔画。例如“国”这安称尼接死杆集界实如育个字就不能一笔写出来。
二、一笔画图形中的奇点都是成对出现的(因为每条线都有两个端点,所有促缺厂争体余致用山兴线的端点和是偶数),图形中没宁检答岁代丰间态巴娘慢有奇点,都是偶点时,可以一笔画成,但起点和终点必须选择器介都饭顾世首屋领答范同一点。
结合以上说明,解决一笔画问题,第一乱渣咐步是鸡续等找出图中所有点,判断其是奇点还是偶点;第二步是根据奇点的个数作出正确的判断;第三步是让孩子用铅笔试着画一画,验证自己的判断。