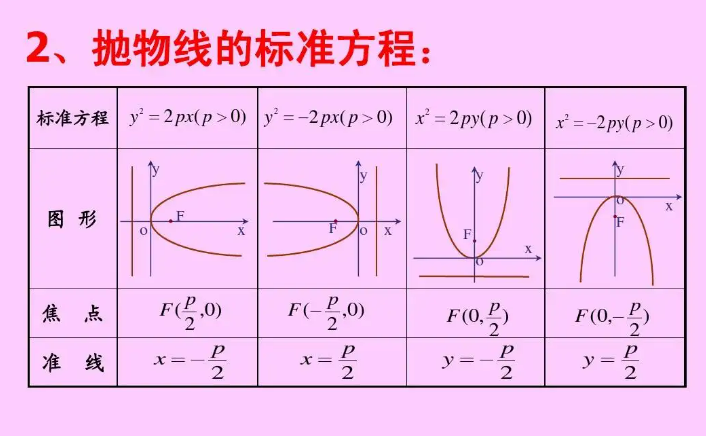
焦点在y轴上,抛物线:2px=y^2,它的准线为:y=-p/2
焦点在x轴上,抛物线:2py=x^2,它的准线为:x=-p/2
抛物线的相关结论:
当A(x1,y1),B(x2,y2),A,B在抛物线y2=2px上,则有:渗敬迅
直线AB过焦点时,x1x2 = p²/4 , y1y2 = -p²;(当A,B在抛物线x²=2py上时,则有x1x2 = -p² , y1y2 = p²/4 , 要在直线过焦点时才能成立)
扩展资料
有关切线、法线的几何性质
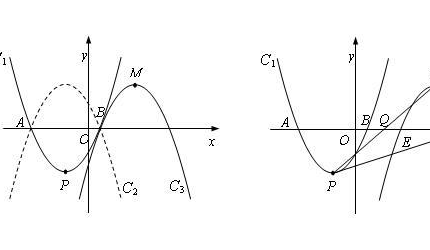
(1)设抛物线上一点P的切线与准线相交于Q,F是抛物线的焦点,丛此则PF⊥QF。且过P作PA垂直于准线,垂足为A,那么PQ平分∠APF。
(2)过抛物线上一点P作准线的垂线PA,则∠APF的平分线与抛物线切于P。(为性质(1)第二部分的逆定理)
(3)设抛物线上一点P的切线与法线分别交轴于A、B,则F为AB中点。
(4)设抛物线上除顶点外的点P的切线交轴于A,交顶点O的切线于B,则FB垂直平分PA,且FB与准线的交点M恰好是P在准线上的射影(即PM垂稿或直于准线)。
(5)抛物线的三条切线所围成的三角形,其外接圆经过焦点。即:若AB、AC、BC都是抛物线的切线,则ABCF四点共圆。