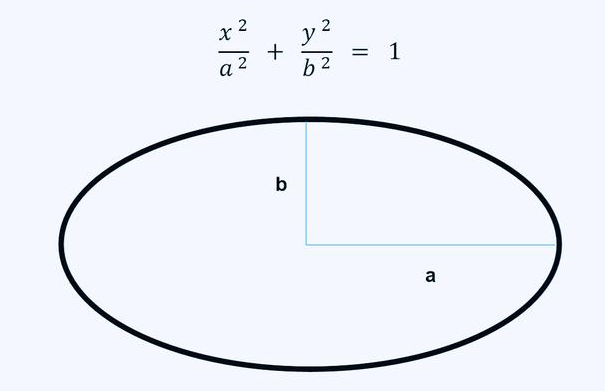
椭圆面积公式是S=π(圆周率)×a×b,其中a、b分别是椭圆的长半轴,短半轴的长或S=π(圆银祥周率)×A×B/4(其中A,B分别是椭圆的长轴,短轴的长)。椭圆面积公式属于几何数学领域。
椭圆是围绕两个焦点的平面中的曲线,使得对于曲线上的每个点,到两个焦点的距离锋源搏之和是恒定的。因此,它是圆的概括,其是具有两个焦点在相同位置处裂裤的特殊类型的椭圆。
椭圆面积用定积分的算法
椭圆面积用定积分算为S=abπ。
解题思路:
设椭圆x^2/a^2+y^2/b^2=1
取第一象限内面积 有 y^2=b^2-b^2/a^2*x^2
即 y=√(b^2-b^2/a^2*x^2)
=b/a*√(a^2-x^2)
由于该式反导数为所求面积,观察到原式为圆方程公式*a/b,根据(af(x))'=a*f'(x),且x=a时圆面积为a^2π/4
可得 当x=a时,1/4S=b/a*1/4*a^2*π=abπ/4
即S=abπ。