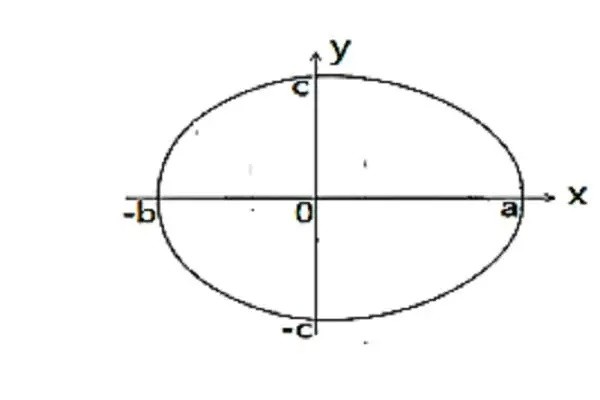
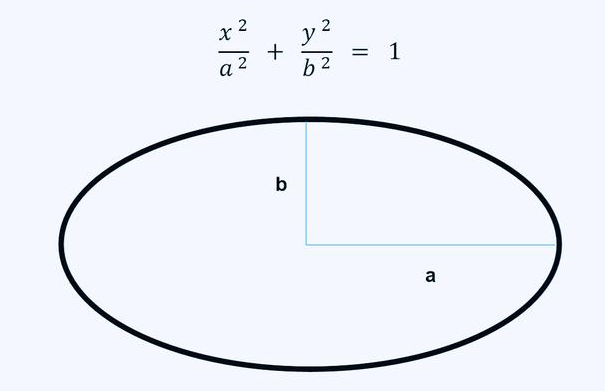
椭圆的面积计算公式是:S=π(圆周率)×a×b(其中a,b分别是椭圆的半长轴,半短轴的长)。或S=π(圆周率)×A×B/4(其中A,B分别是椭圆的长轴,短轴的长)。
一、导数方法
设椭圆x^2/a^2+y^2/b^2=1
取第一象限内面积有y^2=b^2-b^2/a^2*x^2
即y=√(b^2-b^2/a^2*x^2)
由于该式反导数为所求面积,观察到原式为圆方程公式*a/b,根据(af(x))'=a*f'(x),且x=a时圆面积为a^2π/4
可得当x=a时,1/4S=b/a*1/4*a^2*π=abπ/4
即S=abπ。
此配衡方法比较容易理解。
二、阴影面积
众所周知,斜切圆柱所得截面即为椭圆,这在高中数学圆锥曲线一章有阐述,下面就用阴举团影面积法巧妙求解椭圆面积。圆形面积与椭圆面积之比为cosθ,则cosθ=πR^2/S=2R/2a,椭圆短轴b即为圆柱底面半径R,即R=b,所以S=πR^2*a/R=πaR=πab。
三、周长算法
1、第一种:L1=π·qn/atan(n)
(b→a,q=a+b,培答做n=((a-b)/a))^2
这是根据圆周长和割圆术原理推导的,精度一般。